Building a Recommendation Engine with Locality-Sensitive Hashing (LSH) in Python
Learn how to build a recommendation engine in Python using LSH: an algorithm that can handle billions of rows
You will learn:
At the end of this tutorial, the reader can expect to learn how to:
- Examine and prepare data for LSH by creating shingles
- Choose parameters for LSH
- Create Minhash for LSH
- Recommend conference papers with LSH Query
- Build various types of Recommendation Engines using LSH
Introduction to Locality-Sensitive Hashing (LSH) Recommendations
This tutorial will provide step-by-step guide for building a Recommendation Engine. We will be recommending conference papers based on their title and abstract. There are two major types of Recommendation Engines: Content Based and Collaborative Filtering Engines.
- Content Based recommends only using information about the items being recommended. There is no information about the users.
- Collaborative Filtering takes advantage of user information. Generally speaking, the data contains likes or dislikes of every item every user has used. The likes and dislikes could be implicit like the fact that a user watched a whole movie or explicit like the user gave the movie a thumbs up or a good star rating.
In general, Recommendation Engines are essentially looking to find items that share similarity. We can think of similarity as finding sets with a relatively large intersection. We can take any collection of items such as documents, movies, web pages, etc., and collect a set of attributes called "shingles".
Shingles
Shingles are a very basic broad concept. For text, they could be characters, unigrams or bigrams. You could use a set of categories as shingles. Shingles simply reduce our documents to sets of elements that so we can calculate similarity betweens sets.
For our conference papers, we will use unigrams extracted from the paper's title and abstract. If we had data about which papers a set of users liked, we could even use users as shingles. In this way, you could do Item Based Collaborative Filtering where you search a MinHash of items that have been rated positively by the same users.
Likewise, you can flip this idea on its head and make the items the shingles for a User Based Collaborative Filtering. In this case, you would be finding users that had similar positive ratings to another user.
Let's take two paper titles and convert them to sets of unigram shingles:
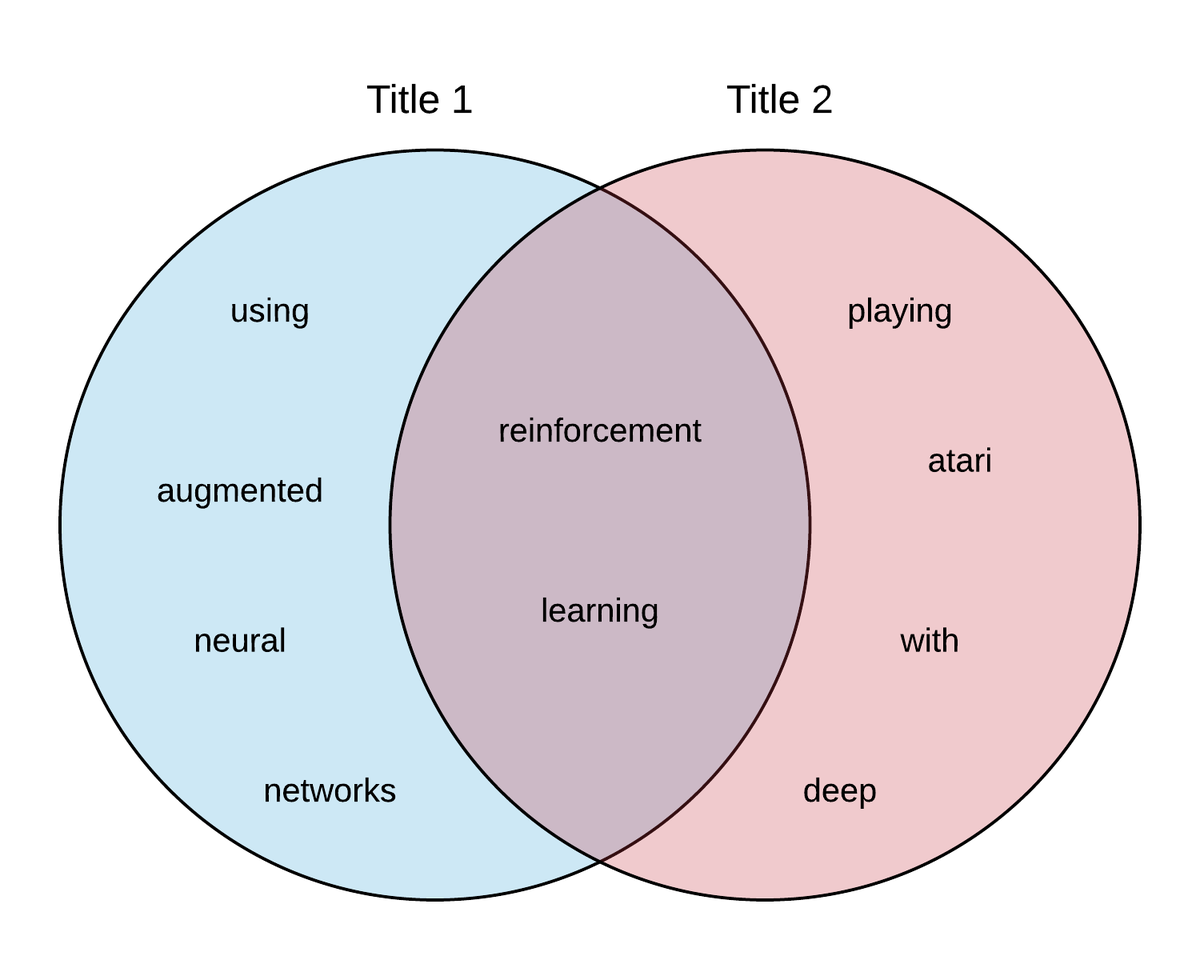
- Title 1 = "Reinforcement Learning using Augmented Neural Networks"
Shingles =['reinforcement', 'learning', 'using', 'augmented', 'neural', 'networks'] - Title 2 = "Playing Atari with Deep Reinforcement Learning"
Shingles =['playing', 'atari', 'with', 'deep', 'reinforcement', 'learning']
Now, we can find the similarity between these titles by looking at a visual representation of the intersection of shingles between the two sets. In this example, the total number (union) of shingles is 10, and 2 are a part of the intersection. We would measure the similarity as 2/10 = 1/5.
Why LSH?
LSH can be considered an algorithm for dimensionality reduction. A problem that arises when we recommend items from large datasets is that there may be too many pairs of items to calculate the similarity of each pair. Also, we likely will have sparse amounts of overlapping data for all items.
To see why this is the case we can consider the matrix of vocabulary that is created when we store all conference papers.
Traditionally, in order to make recommendations we would have a column for every document and a row for every word ever encountered. Since papers can differ widely in their text content, we are going to get a lot of empty rows for each column, hence the sparsity. To make recommendations, we would then compute the similarity between every row by seeing which words are in common.
| paper 1 | paper 2 | paper 3 | ... | paper n | |
|---|---|---|---|---|---|
| word 1 | 1 | 0 | 1 | ... | 0 |
| word 2 | 0 | 0 | 0 | ... | 1 |
| word 3 | 0 | 1 | 1 | ... | 1 |
| ... | |||||
| word n | 1 | 0 | 1 | ... | 0 |
These concerns motivate the LSH technique. This technique can be used as a foundation for more complex Recommendation Engines by compressing the rows into "signatures", or sequences of integers, that let us compare papers without having to compare the entire sets of words.
LSH primarily speeds up the recommendation process compared to more traditional recommendation engines. These models also scale much better. As such, regularly retraining a recommendation engine on a large dataset is far less computationally intensive than traditional recommendation engines. In this tutorial, we walk through an example of recommending similar NIPS conference papers.
Business Use Cases
Recommendation Engines are a very popular. You most likely regularly interact with recommendation engines when you are on your computer, phone, or tablet. We all have had recommendations pushed to us on a number of web applications such as Netflix, Amazon, Facebook, Google, and more. Here are just a few examples of possible use cases:
- Recommending products to a customer
- Predicting Ratings of a product by a customer
- Build consumer groups from survey data
- Recommending next steps in a workflow
- Recommending best practices as a part of a workflow step
- Detecting Plagiarism
- Finding near duplicate Web Pages and Articles
Technical Overview of LSH
LSH is used to perform Nearest Neighbor Searches based on a simple concept of "similarity".
We say two items are similar if the intersection of their sets is sufficiently large.
This is the exact same notion of Jaccard Similarity of Sets. Recall the picture above of similarity. Our final measure of similarity, 1/5, is Jaccard Similarity.
NOTE Jaccard similarity is defined as the intersection of two sets divided by the union of the two sets.
Note, other metrics for similarity can be used, but we will be strictly using Jaccard Similarity for this tutorial. LSH is a type of Neighborhood Based method like k-nearest neighbors (KNN). As you can see in the table below, methods like KNN scale poorly compared to LSH.
| Model Build | Query | |
|---|---|---|
| KNN | ||
| LSH |
$$n: \mbox{number of items}$$
$$p: \mbox{number of permutations}$$
The power of LSH is that it can even scale sub-linearly using a Forest technique as the number of your items grow. As stated before, the goal is to find set(s) similar to a query set.
The general method is to:
- Hash items such that similar items go into the same bucket with high probability.
- Restrict similarity search to the bucket associated with the query item.
Converting Text to a set of Shingles
Remember that a shingle is an individual element that can be a part of a set like a character, unigram or bigram. In the standard literature there is a concept of shingle size, $k$, where the number of shingles is equal to $20^k$. When you choose what your shingles will be, you are implicitly choosing your shingle size.
Lets use the letters of the alphabet as our example of our shingles. You would have 26 shingles. For our alphabet shingles, k = 1 where $20^k$ is approximately the number of distinct characters in the alphabet that are used frequently.
When shingling documents into unigrams, we'll find there's a very large number of possible words, i.e. we'll be using a large value for $k$. The table below gives a quick view of the number of shingles relative to the shingle size, $k$.
| 2 | 400 |
| 3 | 8000 |
| 4 | 160000 |
| 5 | 3200000 |
When it comes to choosing your shingles, you must have enough unique shingles so that the probability of a shingle appearing in a given document is low. If a shingle occurs too frequently accross all of your sets, it will not provide significant differentiation between sets. The classic example in Natural Language Processing (NLP) is the word "the". It is too common. Most NLP work would remove the word "the" from all documents being considered because it does not provide any useful information. Likewise, you don't want to work with shingles that will show up in every set. It reduces the effectiveness of the method. You can also see this idea used with TF-IDF. Terms that appear in too many documents get discounted.
Since you want any individual shingle's probability of appearing in any given document to be low, we may even look at shingles that comprise bigrams, trigrams, or greater. If two documents have a large number of bigrams or trigrams in common, it would indicate those documents are quite similar.
When looking for the proper number of shingles, take a look at the average number of characters or tokens that appear in your documents. Make sure that you choose enough shingles such that there will be significantly more shingles than the average number of shingles in your document.
Example of shingling
For this article, we will be recommending conference papers. As such, we will walk through a quick example with one of the conference paper's titles:
"Self-Organization of Associative Database and Its Applications"
If we use unigrams as shingles, we can remove all punctuation, stopwords, and lowercase all the characters to get the following:
['self', 'organization', 'associative', 'database', 'applications']
Notice we removed common stop words like "of", "and", and "its" since they provide little value.
MinHash Signatures
The goal of the MinHash is to replace a large set with a smaller "signature" that still preserves the underlying similarity metric.
In order to create a MinHash signature for each set:
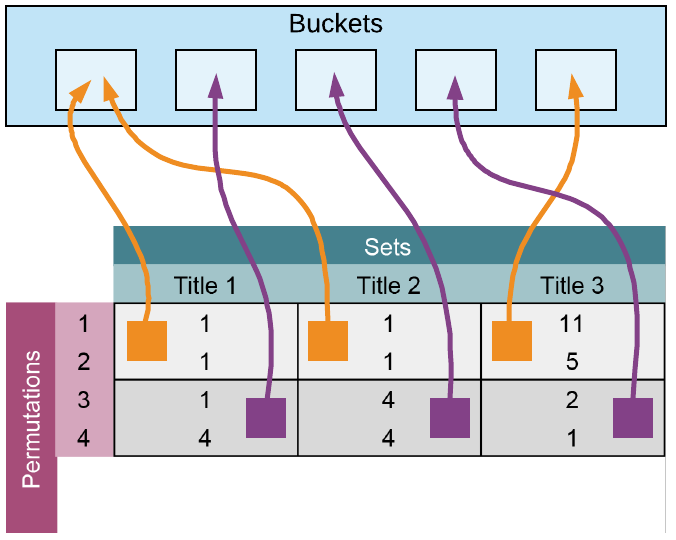
- Randomly permute the rows of the shingle matrix. E.g. Rows 12345 => 35421, so if "reinforcement" was in row 1, it would now be in row 5.
- For each set (paper titles in our case), start from the top and find the position of the first shingle that appears in the set, i.e. the first shingle with a 1 in its cell. Use this shingle number to represent the set. This is the "signature".
- Repeat as many times as desired, each time appending the result to the set's signature.
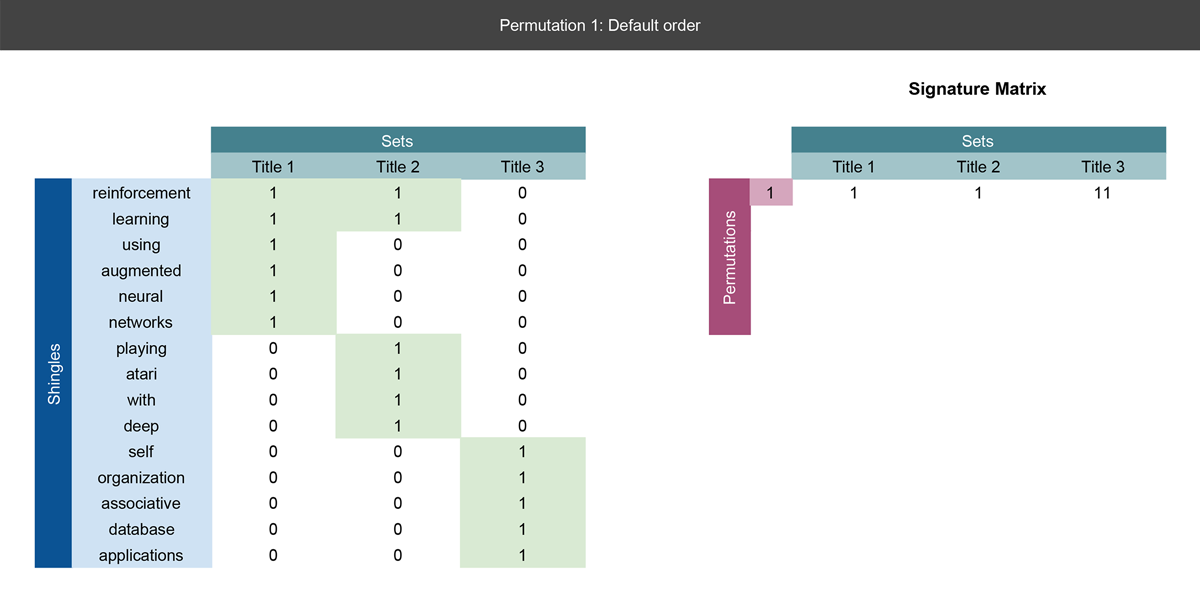
Let's go through a concrete example with the three paper title's we've already mentioned. We've already shingled the titles into sets of unigrams, so we can put them into a matrix and perform all of the steps mentioned above:
Note that in this example we are only using the paper's title for simplicity. In the implementation below we'll also add in the abstract to generate more accurate recommendations.
Slide 1
On the left, we define the matrix with columns as the titles and rows defined as all words encountered in the three titles. If a word appears in a title, we place a 1 next to that word. This will be the input matrix to our hashing function.
Notice our first record in the signature matrix on the right is simply the current row number where we first find a 1. See the next slide for a more detailed explanation.
Slide 2
We perform the first real row permutation. Notice the unigram words have been reordered. Again, we also have the signature matrix on the right where we'll record the result of the permutations.
In each permutation, we are recording the row number of the first word appears in the title, i.e. the row with the first 1. In this permutation, Title 1's and Title 2's first unigram are both in row 1, so a 1 is recorded in row 1 of the signature matrix under Title 1 and 2. For Title 3, the first unigram is in row 5, so 5 is recorded in the first row of the signature matrix under Title 3's column.
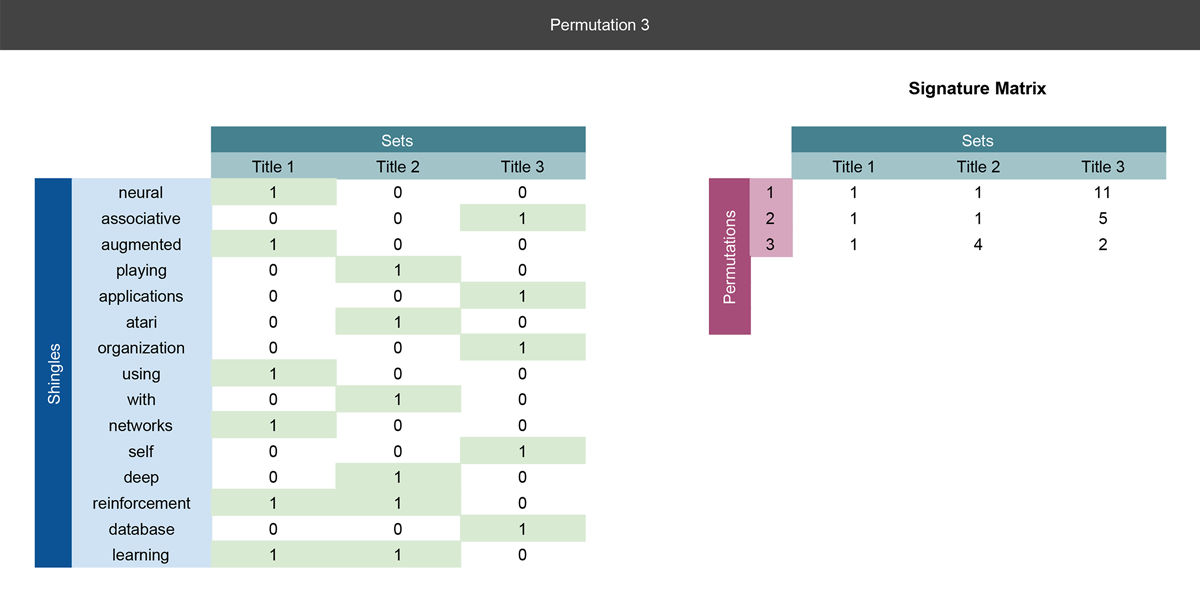
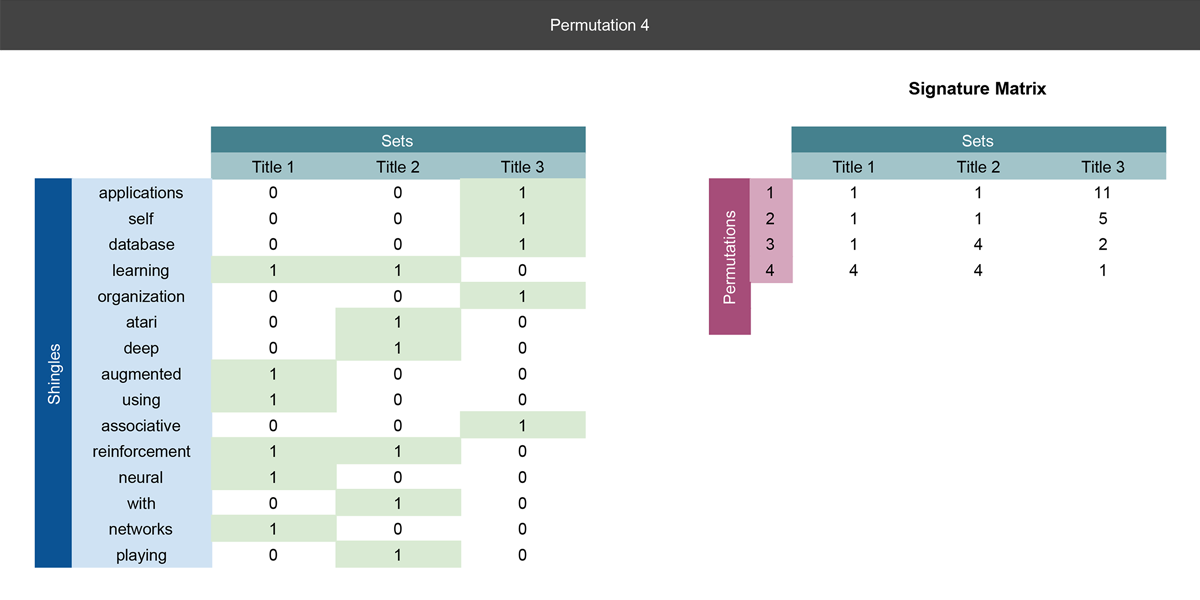
Slides 3-4
We are essentially doing the same operations as Slide 2, but we are creating a new row in the signature matrix for every permutation and putting the result there.
So far we've done three permutations, and we could actually use the signature matrix to calculate the similarity between paper titles. Notice how we have compressed the rows from 15 in the shingle matrix, to 3 in the signature matrix.
After the MinHash procedure, each conference paper will be represented by a MinHash signature where the number of rows is now much less than the number of rows in the original shingle matrix. This is due to us capturing the signatures by performing row permutations. You should need far fewer permutations than actual shingles.
Now if we think about all words that could appear in all paper titles and abstracts, we have potentially millions of rows. By generating signatures through row permutations, we can effectively reduce the rows from millions to hundreds without loss of the ability to calculate similarity scores.
Obviously, the more you permute the rows, the longer the signature will be. This provides us with the end goal where similar conference papers have similar signatures. In fact, you can observe the following:
$$P(h(\mbox{Set 1})) = P(h(\mbox{Set 2})) = \mbox{jaccard_sim} (\mbox{Set 1, Set 2})\mbox{,}$$
$$\mbox{ where h is the MinHash of the set}$$
In order to be more efficient, random hash functions are used instead of random permutations of rows when done in practice.
LSH on MinHash Signatures
The signature matrix above is now divided into $b$ bands of $r$ rows each, and each band is hashed separately. For this example, we are setting band $b = 2$, which means that we will consider any titles with the same first two rows to be similar. The larger we make b the less likely there will be another Paper that matches all of the same permutations.
For example, notice the first band on the matrix above, conference paper Title 1 and conference paper Title 2 will end up in the same bucket since they both have the same bands, whereas Title 3 is totally different. Even though the ends of Title 1 and 2's signatures differ, they are still bucketed together and considered similar with our band sizing.
Ultimately, the size of the bands control the probability that two items with a given Jaccard similarity end up in the same bucket. If the number of bands is larger, you will end up with much smaller sets. For instance, $b = p$, where p is the number of permutations (i.e. rows in the signature matrix) would almost certainly lead to N buckets of only one item because there would be only one item that was perfect similar across every permutation. What we are really looking for when we select the band size is for our tolerance for false positives (no similar documents ending up in the same bucket) and false negatives (similar documents not ending up in the same bucket).
Querying for Recommendations
When a new query is made, we use the following procedure:
- Convert the query text to shingles (tokens).
- Apply MinHash and LSH to the shingle set, which maps it to a specific bucket.
- Conduct a similarity search between the query item and the other items in the bucket.
Efficiencies can be achieved by actually using an LSH Forest algorithm for efficient searching. For more info, see M. Bawa, T. Condie and P. Ganesan, "LSH Forest: Self-Tuning Indexes for Similarity Search.
LSH Checklist
As a final checklist for performing LSH, ensure that you complete the following steps:
- Create shingles from your available data set (e.g. unigrams, bigrams, ratings, etc.)
- Build an $m \times n$ shingle matrix where every shingle that appears in a set is marked with a 1 otherwise 0.
- Permute the rows of the shingle matrix from step 2 and build a new $p \times n$ signature matrix where the number of the row of the first shingle to appear for a set is recorded for the permutation of the signature matrix.
- Repeat permuting the rows of the input matrix $p$ times and complete filling in the $p \times n$ signature matrix.
- Choose a band size $b$ for the number of rows you will compare between sets in the LSH matrix.
Implementing LSH in Python
Step 1: Load Python Packages
Step 2: Exploring Your Data
Our goal in this tutorial is to make recommendations on conference papers by using LSH to quickly query all of the known conference papers. As a general rule, you should always examine your data. You need a thorough understanding of the dataset in order to properly pre-process your data and determine the best parameters. We have given some basic guidelines for selecting parameters, and they all require an exploration of your dataset as described above.
For the purposes of this tutorial, we will be working with an easy dataset. Kaggle has the "Neural Information Processing Systems (NIPS) conference papers. You can find them here.
An initial data exploration of these papers can be found here.
Step 3: Preprocess your data
For the purposes of this article, we will only use a rough version of unigrams as our shingles. We use the following steps:
- Remove all punctuation.
- Lowercase all text.
- Create unigram shingles (tokens) by separating any white space.
For better results, you may try using a natural language processing library like NLTK or spaCy to produce unigrams and bigrams, remove stop words, and perform lemmatization.
You can see a quick example of the preprocessing step below.
Step 4: Choose your parameters
To start our example, we will use the standard number of permutations of 128. We will also start by just making one recommendation.
Step 5: Create Minhash Forest for Queries
In order to create the Minhash Forest, we will execute the following steps:
- Pass in a dataframe with every string you want to query.
- Preprocess a string of text using our preprocessing step above.
- Set the number of permutations in your MinHash.
- MinHash the string on all of your shingles in the string.
- Store the MinHash of the string.
- Repeat 2-5 for all strings in your dataframe.
- Build a forest of all the MinHashed strings.
- Index your forest to make it searchable.
Step 6: Evaluate Queries
In order to query the forest that was built, we will follow the steps below:
- Preprocess your text into shingles.
- Set the same number of permutations for your MinHash as was used to build the forest.
- Create your MinHash on the text using all your shingles.
- Query the forest with your MinHash and return the number of requested recommendations.
- Provide the titles of each conference paper recommended.
Testing Our Recommendation Engine on NIPS Conference Papers
We will start by loading the CSV containing all the conference papers and creating a new field that combines the title and the abstract into one field, so we can build are shingles using both title and abstract.
Finally, we can query any string of text such as a title or general topic to return a list of recommendations. Note, for our example below, we have actually picked the title of a conference paper. Naturally, we get the exact paper as one of our recommendations.
Conclusions
Just as a quick final note, you can build numerous recommendation engines with this method. You do not have to be limited to just Content Based Filtering as we demonstrated. You can also use these techniques for Collaborative Filtered Recommendation Engines.
To summarize, the procedures outlined in this tutorial represent an introduction to Locality-Sensitive Hashing. Materials here can be used as a general guideline. If you are working with a large number of items and your metric for similarity is that of Jaccard similarity, LSH offers a very powerful and scalable way to make recommendations.